Digite uma palavra ou frase em qualquer idioma 👆
Idioma:
Tradução e análise de palavras por inteligência artificial ChatGPT
Nesta página você pode obter uma análise detalhada de uma palavra ou frase, produzida usando a melhor tecnologia de inteligência artificial até o momento:
- como a palavra é usada
- frequência de uso
- é usado com mais frequência na fala oral ou escrita
- opções de tradução de palavras
- exemplos de uso (várias frases com tradução)
- etimologia
O que (quem) é Знаки математические - definição
ВЕЛИЧИНА, ЗНАЧЕНИЕ КОТОРОЙ НЕ МЕНЯЕТСЯ; В ЭТОМ ОНА ПРОТИВОПОЛОЖНА ПЕРЕМЕННОЙ
Математические константы
Знаки математические
условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. Например, √2
(квадратный корень из двух), 3 > 2 (три больше двух) и т.п.
Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первыми З. м. были знаки для изображения чисел - Цифры, возникновение которых, по-видимому, предшествовало письменности. Наиболее древние системы нумерации - вавилонская и египетская - появились ещё за 31/2 тысячелетия до н. э.
Первые З. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Величины (площади, объёмы, углы) изображались в виде отрезков, а произведение двух произвольных однородных величин - в виде прямоугольника, построенного на соответствующих отрезках. В "Началах" Евклида (3 в. до н. э.) величины обозначаются двумя буквами - начальной и конечной буквами соответствующего отрезка, а иногда и одной. У Архимеда (3 в. до нашей эры) последний способ становится обычным. Подобное обозначение содержало в себе возможности развития буквенного исчисления. Однако в классической античной математике буквенного исчисления создано не было.
Начатки буквенного изображения и исчисления возникают в позднеэллинистическую эпоху в результате освобождения алгебры от геометрической формы. Диофант (вероятно, 3 в.) записывал неизвестную (х) и её степени следующими знаками:
[ - от греческого термина δυναμις (dynamis - сила), обозначавшего квадрат неизвестной,
- от греческого термина δυναμις (dynamis - сила), обозначавшего квадрат неизвестной,  - от греческого χυβος (k_ybos) - куб]. Справа от неизвестной или её степеней Диофант писал коэффициенты, например 3х5 изображалось
- от греческого χυβος (k_ybos) - куб]. Справа от неизвестной или её степеней Диофант писал коэффициенты, например 3х5 изображалось
(где  = 3). При сложении Диофант приписывал слагаемые друг к другу, для вычитания употреблял специальный знак
= 3). При сложении Диофант приписывал слагаемые друг к другу, для вычитания употреблял специальный знак 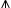 ; равенство Диофант обозначал буквой ι [от греческого ισος (isos) - равный]. Например, уравнение
; равенство Диофант обозначал буквой ι [от греческого ισος (isos) - равный]. Например, уравнение
 ; равенство Диофант обозначал буквой ι [от греческого ισος (isos) - равный]. Например, уравнение
; равенство Диофант обозначал буквой ι [от греческого ισος (isos) - равный]. Например, уравнение (x3 + 8x) - (5x2 + 1) = х
у Диофанта записалось бы так:
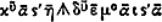
(здесь 
означает, что единица  не имеет множителя в виде степени неизвестного).
не имеет множителя в виде степени неизвестного).
Несколько веков спустя индийцы ввели различные З. м. для нескольких неизвестных (сокращения наименований цветов, обозначавших неизвестные), квадрата, квадратного корня, вычитаемого числа. Так, уравнение
3х2 + 10x - 8 = x2 + 1
в записи Брахмагупты (См. Брахмагупта) (7 в.) имело бы вид:
йа ва 3 йа 10 ру 8
йа ва 1 йа 0 ру 1
(йа - от йават - тават - неизвестное, ва - от варга - квадратное число, ру - от рупа - монета рупия - свободный член, точка над числом означает вычитаемое число).
Создание современной алгебраической символики относится к 14-17 вв.; оно определялось успехами практической арифметики и учения об уравнениях. В различных странах стихийно появляются З. м. для некоторых действий и для степеней неизвестной величины. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный символ. Так, в конце 15 и. Н. Шюке и Л. Пачоли употребляли знаки сложения и вычитания
(от лат. plus и minus), немецкие математики ввели современные + (вероятно, сокращение лат. et) и -. Ещё в 17 в. можно насчитать около десятка З. м. для действия умножения.
Различны были и З. м. неизвестной и её степеней. В 16 - начале 17 вв. конкурировало более десяти обозначений для одного только квадрата неизвестной, например се (от census - латинский термин, служивший переводом греческого δυναμις, Q (от quadratum),  , A (2),
, A (2),  , Aii, aa, a2 и др. Так, уравнение
, Aii, aa, a2 и др. Так, уравнение
x3 + 5x = 12
имело бы у итальянского математика Дж. Кардано (1545) вид:
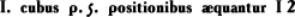
у немецкого математика М. Штифеля (1544):
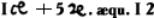
у итальянского математика Р. Бомбелли (1572):
французского математика Ф. Виета (1591):
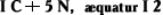
у английского математика Т. Гарриота (1631):
В 16 и начале 17 вв. входят в употребление знаки равенства и скобки: квадратные (Р. Бомбелли, 1550), круглые (Н. Тарталья, 1556), фигурные (Ф. Виет, 1593). В 16 в. современный вид принимает запись дробей.
Значительным шагом вперёд в развитии математической символики явилось введение Виетом (1591) З. м. для произвольных постоянных величин в виде прописных согласных букв латинского алфавита В, D, что дало ему возможность впервые записывать алгебраические уравнения с произвольными коэффициентами и оперировать ими. Неизвестные Виет изображал гласными прописными буквами А, Е,... Например, запись Виета
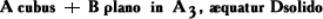
[cubus - куб, planus - плоский, т. е. В - двумерная величина; solidus - телесный (трёхмерный), размерность отмечалась для того, чтобы все члены были однородны] в наших символах выглядит так:
x3 + 3bx = d.
Виет явился творцом алгебраических формул. Р. Декарт (1637) придал знакам алгебры современный вид, обозначая неизвестные последними буквами лат. алфавита х, у, z, а произвольные данные величины - начальными буквами а, b, с. Ему же принадлежит нынешняя запись степени. Обозначения Декарта обладали большим преимуществом по сравнению со всеми предыдущими. Поэтому они скоро получили всеобщее признание.
Дальнейшее развитие З. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики которого основа была уже в большой мере подготовлена в алгебре.
Даты возникновения некоторых математических знаков
И. Ньютон в своём методе флюксий и флюент (1666 и следующие гг.) ввёл знаки для последовательных флюксий (производных) величины (в виде
и для бесконечно малого приращения o. Несколько ранее Дж. Валлис (1655) предложил знак бесконечности ∞.
Создателем современной символики дифференциального и интегрального исчислений является Г. Лейбниц. Ему, в частности, принадлежат употребляемые ныне З. м. дифференциалов
dx, d 2x, d 3x
и интеграла
Огромная заслуга в создании символики современной математики принадлежат Л. Эйлеру. Он ввёл (1734) в общее употребление первый знак переменной операции, именно знак функции f (x) (от лат. functio). После работ Эйлера знаки для многих индивидуальных функций, например тригонометрических, приобрели стандартный характер. Эйлеру же принадлежат обозначения постоянных е (основание натуральных логарифмов, 1736), π [вероятно, от греческого περιφερεια (periphereia) - окружность, периферия, 1736], мнимой единицы
(от французского imaginaire - мнимый, 1777, опубликовано в 1794).
В 19 в. роль символики возрастает. В это время появляются знаки абсолютной величины |x| (К. Вейерштрасс, 1841), вектора r̅ (О. Коши, 1853), определителя
(А. Кэли, 1841) и др. Многие теории, возникшие в 19 в., например Тензорное исчисление, не могли быть развиты без подходящей символики.
Наряду с указанным процессом стандартизации З. м. в современной литературе весьма часто можно встретить З. м., используемые отдельными авторами только в пределах данного исследования.
С точки зрения математической логики, среди З. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений. Например, знаки 1, 2, 3, 4 изображают числа, т. е. объекты, изучаемые арифметикой. Знак операции сложения + сам по себе не изображает никакого объекта; он получает предметное содержание, когда указано, какие числа складываются: запись 1 + 3 изображает число 4. Знак > (больше) есть знак отношения между числами. Знак отношения получает вполне определённое содержание, когда указано, между какими объектами отношение рассматривается. К перечисленным трём основным группам З. м. примыкает четвёртая: Г) вспомогательные знаки, устанавливающие порядок сочетания основных знаков. Достаточное представление о таких знаках дают скобки, указывающие порядок производства действий.
Знаки каждой из трёх групп А), Б) и В) бывают двух родов: 1) индивидуальные знаки вполне определённых объектов, операций и отношений, 2) общие знаки "неременных", или "неизвестных", объектов, операций и отношений.
Примеры знаков первого рода могут служить (см. также таблицу):
A1) Обозначения натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9; трансцендентных чисел е и π; мнимой единицы i.
Б1) Знаки арифметических действий +, -, ·, ×,:; извлечения корня  , дифференцирования
, дифференцирования
знаки суммы (объединения) ∪ и произведения (пересечения) ∩ множеств; сюда же относятся знаки индивидуальных функций sin, tg, log и т.п.
B1) Знаки равенства и неравенства =, >, <, ≠, знаки параллельности || и перпендикулярности ⊥, знаки принадлежности ∈ элемента некоторому множеству и включения ⊂ одного множества в другое и т.п.
Знаки второго рода изображают произвольные объекты, операции и отношения определённого класса или объекты, операции и отношения, подчинённые каким-либо заранее оговорённым условиям. Например, при записи тождества (a + b)(a - b) = a2 - b2 буквы а и b обозначают произвольные числа; при изучения функциональной зависимости у = х2 буквы х и у - произвольные числа, связанные заданным отношением; при решении уравнения
x2 - 1 = 0
х обозначает любое число, удовлетворяющее данному уравнению (в результате решения этого уравнения мы узнаём, что этому условию соответствуют лишь два возможных значения +1 и -1).
С логической точки зрения, законно такого рода общие знаки называть знаками переменных, как это принято в математической логике, не пугаясь того обстоятельства, что "область изменения" переменного может оказаться состоящей из одного единственного объекта или даже "пустой" (например, в случае уравнений, не имеющих решения). Дальнейшими примерами такого рода знаков могут служить:
A2) Обозначения точек, прямых, плоскостей и более сложных геометрических фигур буквами в геометрии.
Б2) Обозначения f, F, φ для функций и обозначения операторного исчисления, когда одной буквой L изображают, например, произвольный оператор вида:
Обозначения для "переменных отношений" менее распространены, они находят применение лишь в математической логике (см. Алгебра логики) и в сравнительно абстрактных, по преимуществу аксиоматических, математических исследованиях.
Лит.: Cajori F., A history of mathematical notations, v. 1-2, Chi., 1928-29.
ЗНАКИ МАТЕМАТИЧЕСКИЕ
условные обозначения, служащие для записи математических понятий, предложений и выкладок. Напр., математические знаки +, -, =, > (больше), (знак корня), sin (синус), (интеграл) и т. д. Первыми знаками математическими, возникшими за 31/2 тысячелетия до н. э., были знаки для изображения чисел - цифры. Создание современной математической символики относится к 14-18 вв.
Метро 2033: Путевые знаки
РОМАН ВЛАДИМИРА БЕРЕЗИНА В СЕРИИ «ВСЕЛЕННАЯ МЕТРО 2033»
Путевые знаки; Путевые знаки (роман); Метро 2033. Путевые знаки
«Метро 2033: Путевые знаки» — постапокалиптический роман Владимира Березина, изданный в декабре 2009 года. Первая книга в серии «Вселенная Метро 2033», повествующей о жизни некоторых регионов Земли после ядерной войны и вдохновлённой романами Дмитрия Глуховского «Метро 2033» и «Метро 2034».
Wikipédia
Математическая константа
Математическая константа или математическая постоянная — величина, значение которой не меняется; в этом она противоположна переменной. В отличие от физических постоянных, математические постоянные определены независимо от каких бы то ни было физических измерений.


